Question from Aubrey, a secondary school student:

finding the legth of a guy wire:
a radio tower 500 feet high is located on the side of a hill with an inclination to the horizontal of 5 degrees. how long should two guy wires be if they are to connect to the top of the tower and be secured at two points 100 feet directly above and directly below the base of the tower?

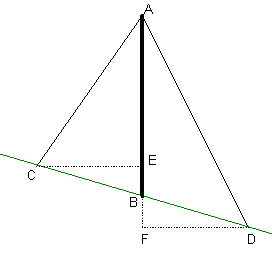
Hi Aubrey.

The first thing I always do with word problems in trigonometry is draw a picture, label the interesting parts and add extra lines where I think they'll be useful.

Line segment AB is the tower, AC and AD are the guy-wires and slope CD is the hill. So the length of AB is 500 ft and we want to know the lengths AC and AD.

I've also drawn point E so that EB is 100 ft long and point F so that BF is 100 ft long.

You are also given the fact that the hill is a 5 degree slope,
so BDF = ECB = 5 degrees.

Start by looking at BFD. It's a right triangle and you know one angle, so you can figure out the other easily. You also know one length, so you can figure out the length of the hypotenuse using any of the usual trig functions (sine, cosine or tangent) with the length BF and the appropriate angle. That gives you the length BD.

Now look at angle ABD. It is the supplementary angle to angle FBD, which you figured out already, so you know the length AB (500), the length BD (the hypotenuse from the last paragraph), and the angle in between them. So you can use the Law of Cosines to find the length AD, the right-hand guy-wire.

Now use the same ideas to figure out the left side of the diagram. You won't need the Law of Cosines for this side, just a simple application of Pythagorus' Theorem is enough.

Hope this helps,
Stephen La Rocque.