Subject: Rate
Name: Cassie
Who are you: Student

A boat is being pulled towards a dock. If the rope is being pulled in at 3 feet per second, how fast is the distance between the dock and the boat decreasing when it is 30 feet from the dock?

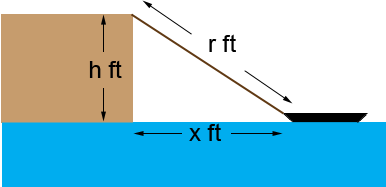
Hi Cassie,

I think there is something missing from your problem. If the rope is on the same level as the boat then the boat is moving at 3 feet per second. I expect that there is a dock a certain height (say h feet) above the level of the water as in the diagram.

In the diagram x is the distance from the boat to the dock and r is the length of the rope, both in feet. h is a constant height, r and x are functions of time t, r is decreasing at the rate of 3 ft/sec and you want to know the rate that x is decreasing when x is 30 ft.

The triangle formed by the dock, the water and the rope is a right triangle and hence, by Pythagoras theorem,

h² + x² = r²

Differentiating both sides with respect to t gives

2 x ^dx/_dt = 2 r ^dr/_dt

 Can you finish the problem?

Penny