Subject: Trig question
Name: Christina
Who are you: Student

I'm have a hard time solving cos2x=1 for exact values between 0<_x <360

 

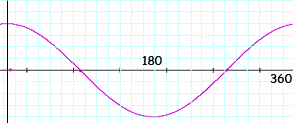
We have two responses for you.

Hi Christina,

I drew a rough sketch of y = cos t for 0 ≤ t ≤ 360 degrees. You can see from the graph that cos t = 1 if t = 0 or t = 360.

You also know from the periodic nature of the cosine function that cos t = 1 if
t = 0, t = 360, t = 2 x 360 = 720, ...

Thus for your function cos 2x = 1 if 2x = 0, 2x = 360, 2x = 2 x 360 = 720, .... That is x = 0, x = 180, x = 360, ... But you only want values of x that satisfy 0 ≤ x < 360 and hence the only values are x = 0 degrees and x = 180 degrees.

Penny

Hi Christina.

Try substituting for 2x.

Let theta = 2x. Then cos theta = cos 2x. Also, x = theta/2.

So if 0 <= x < 360, then 0 <= theta/2 < 360, which means 0 <= theta < 720.

Now within the range of 0 <= theta < 720, for what values of theta is cos theta = 1?

You can sketch a cosine curve if you can't answer immediately, or look in your textbook for one.

Now that you know all the value(s) of theta, recall that x = theta/2, so you can find each corresponding value for x.

Hope this helps,
Stephen La Rocque. >