Hi Christopher.

First, I assume you mean a regular octagon (one where all the angles and sides are equal). What you need is an equation that relates the side length (call it x) to the area. Let's draw it and divide up the octagon into pieces:

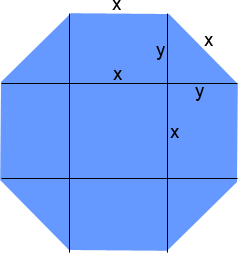
I've labelled the side length as x and another length that is useful to us as y.

By symmetry, you should be able to discern that the four triangles add up to the same as 2 squares of side length y, so that is 2y² . The central square is of course x² . And the four rectangles are 4xy. That makes the total area (A) of the octagon:

A = 2y² + x² + 4xy

You know the area you want, but there are two other unknowns here: x and y, so we need to rewrite one in terms of the other. Take a closer look at one of those triangles. It is a right triangle and so Pythagorus' Theorem applies. That means x² = 2y² or in other words, y = x/√2. That in turn means that

A = x ² + x² + 4x² /√2 = x² (2+2√2)

If we re-arrange this to solve for x, we get this:

Now you can finally plug in 10 000 for the area A and find the appropriate side length x.

Hope this helps,
Stephen La Rocque.