|
 |
|
Subject: Truncated cone calculations I'm interested in calculating cone information regarding motorcycle expansion chamber design for example. I guess it's called a truncated cone, from what I've read so far. If I know the center line height, small radius, and large radius of a truncated cone then, how can I calculate the angle (included angle?) the cone forms? I'd like to know the variations of the formula so I can calculate for angle, or length, or one of the diameters if I know the other two measurements.
|
|
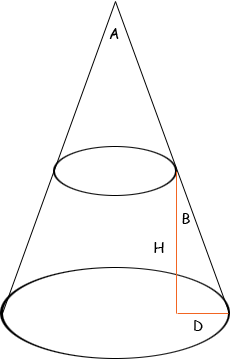
Hi David. You can draw a right triangle with the difference in radii (call it D) as one side, the center line height (call it H) as the perpendicular side and the hypotenuse as the sloped side of the chamber. Thus, if we put D on the bottom, then the ratio D/H is the tangent of the angle B which is opposite D, which is half the included angle of the cone (if we define this to be double the angle rotated around the vertical axis; probably what you intend). So if the included angle is A, then tan(A/2) = D/H or equivalently, arctan(D/H) = A/2. (The function arctan might be called tan-1 on your calculator.)
This only will work for a right-circular cone, but it sounds like that is what you are describing. Hope this is helpful, |
 |
 |
 |