Subject: AP calculus
Name: Ellen
Who are you: Student

consider the curve -8x² +5xy+y³ +149 =0
Write an equation for the line tangent to the curve at (4, -1)
use this equation to approximate the value of K at the point (4.2, K)
Thanks!

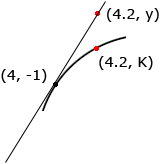
Hi Ellen,

First you need to use implicit differentiation to find the derivative  ^dy/_dx and evaluate it at the point (4, -1) on the curve. Use this value of the slope of the tangent to the curve at (4, -1) to find the equation of the tangent line.

For the second part of the problem the goal is to find the point on the curve which has
x = 4.2, the author calls this point (4.2, K). This is not as straightforward as it looks since if you substitute x = 4.2 into the equation of the curve you get a cubic equation in y. You can however approximate K using the tangent line you found above.

If you magnify the portion of the curve close to (4, -1) you see that the curve and the tangent line are very close to each other,

and hence the points (4.2, K) on the curve and (4.2, y) on the tangent line are very close together. Thus you can substitute x = 4.2 into the equation of the tangent line to find y which is then approximately equal to K.

I hope this helps,
Penny