Subject: Area of an octagon
Name: Farhana
Who are you: Other

I have a regular octagon with sides of 0.8m and I need to find the area,
please help

 

Farhana,

There is a very useful property of area that can be used to solve your problem. The property is that

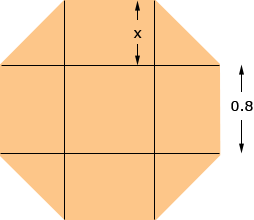
if you subdivide a region into non-overlapping pieces then the area of the region is the sum of the areas of the individual pieces.

For your regular octagon I want to subdivide it into a square, four rectangles and four isosceles right triangles as in the diagram.

  • The area of the square is 0.82 m2 = 0.64 m2.

  • The area of each rectangle is 0.8 x x m2.

Since each triangle has base of length x m and height x m

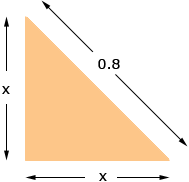
  • the area of each triangle is 1/2 x x x m2.

All that remains is to find x.

Look at one of the triangles.

Each triangle is an isosceles right triangle with legs of length x m and hypotenuse of length 0.8 m. Thus by Pythagoras Theorem

x2 + x2 = 0.82 so
2 x2 = 0.64 and hence x = √0.32 = 0.57 m

Thus the area of the octagon is

0.64 + 4 x 0.8 x x + 4 x 1/2 x x x m2

where x = 0.57 m.

Penny

Karen points out that there is more than one way to find the area.

Hello!

We have answered a question like this before! There are two methods that will help you find the area of an octagon. You will just have to apply one of the methods to your 0.8m regular octagon! The trick is to divide the shape into different pieces that you already know how to calculate the area of. I hope this helps!

mathcentral.uregina.ca/QQ/database/QQ.09.04/jeremy2.html

mathcentral.uregina.ca/QQ/database/QQ.09.01/laurie2.html

Goodluck,

Karen