Amitesh,

I am afraid we are not going to be of any help. The volume of a container depends on the dimensions and shape and there is no general way to calculate this volume. Each calculation is different and depends on the lengths of the sides, the angles at which the sides come together, whether the sides are flat or curved etc. Even then the tonnage depends on the material being placed in the container. For example a container full of dry sand weighs approximately twice as much as the same container filled with wheat.

Harley

Amitesh replied,

Dear Sir,

Thanks for your prompt response. I am very much agree with your point of contention. But if you consider a generalized view, still you will be able to answer my question. For example:- suppose considering a rectangular hopper of length 8 m, height 12 m, width 4 m, plate thickness of 6 mm and at the bottom portion of the hopper having valley angle of 14 deg. and density of material is 7.28. Considering this dimension is it possible for you to send the schematic drawing and the tonnage calculation for the referred dimension.
Looking forward to your response.

Thanks & regards

Amitesh

I drew a rough sketch (not to scale) of what I understand is your hopper.

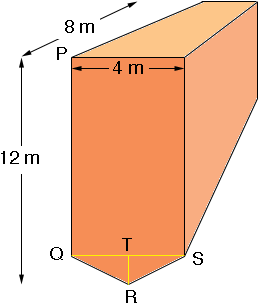
From your description I think that the angle TQR is 14 degrees. Thus triangle TQR is a right triangle with |TQ| = 2 m so |TR| = 2 tan(14^o) = 0.5 m.

Hence your hopper is composed of a rectangular box 8 m by 11.5 m by 4 m with a piece at the bottom that is 8 m long and has a triangular cross- section (triangle RQR). The rectangular box has volume

8 11.5 4 = 368 cubic metres

The triangle SQR has area 1/2 base time height = 1/2 4 0.5 = 1 square metre and hence the bottom piece of the hopper has a volume of

1 8 = 8 cubic metres.

Hence the volume of the hopper is

368 + 8 = 376 cubic metres.

You told us the density of the material in the hopper is 7.28 but you didn't supply units. If necessary convert the density to weight units per cubic metre and multiply by 376 to obtain the weight.

I have ignored the plate thickness in my calculations as I think it will make very little difference in the final result. If you want to include the plate thickness the reduce the length, with and height of the hopper by
2 6 mm = 12 mm and redo the calculations.

Harley