 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
I am an art student making a piece of jewelry out of a flat metal sheet. I'm trying to make a long narrow cone that's roughly 3 1/4" long and just slightly under 1" wide at the base. Since I'm no math wiz, I'm having a |
Hi Amy,
I drew a picture of the cone as I see it
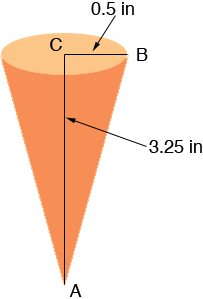
Triangle ABC is a right triangle and hence Pythagoras' theorem tell us
|BC|2 + |CA|2 = |AB|2
so
0.52 + 3.252 = |AB|2 so |AB| = 3.29 inches
Hence when the cone is slit and rolled out it is a sector of a circle of radius 3.39 inches.
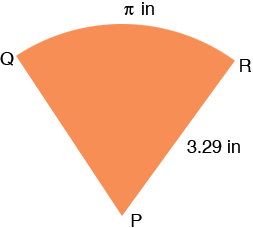
The length of the arc RQ is the circumference of the circle at the base of the cone. This circle has a radius of 0.5 inches and the circumference of a circle is 2 
r and hence the length of the arc RQ is inches.
What remains is to find the measure of the angle RPQ. The circumference of the circle containing the arc RQ is
2
3.29 = 20.67 inches.
The length of arc RQ is only a fraction of this length, in fact the fraction is /20.67 and hence the angle RPQ is the same fraction of 360 degrees. Thus the measure of the angle RPQ is
I hope this helps,
Penny
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.