| |||
| Math Central | Quandaries & Queries |
|
We have two responses for you Question from Ann, a parent: Please help with solving the following problem!!! A circle is inscribed in an equilateral triangle with a side of length 2. Three circles are drawn externally tangent to this circle and internally tangent to 2 sides of the triangle. 3 more circles are drawn externally tangent to these circles and internally tangent to 2 sides of the triangle. if this process continued forever, what would be the sum of the areas of all the circle? the answer 1 parent came up with was Pie over 2, but we don't know how he did it. Can you please show the work or explain the answer to this problem? Thank you Ann p s my daughter is in 9th grade math. |
Hi Ann,
We started with an equilateral triangle of side length a, so the length of PR is a.
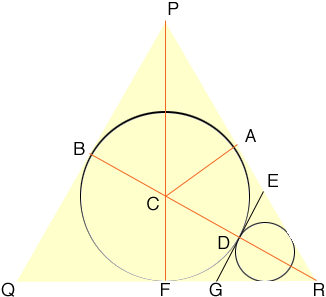
The triangle PFR is a 30-60-90 triangle so the side lengths ore in the proportions 1:2:√3. Since the length of PR is a the length of FR is a/2 and the length of PF is √3 a/2. Let the radius of the first circle, the one with centre C be r1. Since the triangle PCA is a right triangle I can use Pythagoras' theorem to write
r12 + (a/2)2 = (√3 a/2 - r1)2
Expand and simplify to get r1 = a/(2 √3).
Now turn your attention to triangle EGR and the next circle. The length of BR is equal to the length of PF which is √3 a/2. Thus the length of DR is √3 a/2 - 2r1 = a/(2 √3). This is the height of the triangle EGR. Notice that this is one third of the height of the triangle PQR. Thus the radius r2 of the second circle is one third of r1. Likewise the radius r3 of the third circle (not on the diagram) is one third of r2. Thus the radius of the n+1st circle is
rn+1= a/(2 √3) (1/3n)
Hence the area of the n+1st circle is
An+1 = π a2/(12 × 9n)
The area you want is thus
A1 plus 3 times the sum of An+1 for n = 1 to ∞.
This sum is a geometric series which your daughter will be able to evaluate. When we did it we got the final answer to be 11 π/24.
Penny and Sue
Ann,
The answer to this question touches on ideas about infinity that are well beyond grade 9. I assume that the procedure intends to inscribe the largest possible circle in all the gaps between circles of the previous step (so you use one circle in step 1, 3 circles in step 2, 9 circles in step 3, 27 circles in step 4, and so on). In this way the new inscribed circles are tangent to the sides of each empty triangular region of the previous step, where some of these regions have curved sides.
The area covered by the circles equals the area of the whole triangle, namely half base times height
= (1/2)*2*sqrt(3)
= sqrt(3)).
Intuitively, every positive piece of area is eventually covered by a circle. (The fact that infinitely many points remain uncovered is what makes the problem advanced. It turns out that these missing infinitely many points add nothing to the area covered by the triangle that is outside the circles.)
Chris
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.