 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Arnold: I am making a metal shroud for a outdoor fireplace, it is basically a lampshade type pattern,like the bottom of a cone.The top has to be 6 inches to fit the 6 inch stovepipe,and the bottom will be a 24 inch circle. the sides will be 18 inches in length.With the cost of the sheet metal,I can only afford to cut this out once,can you help me with the pattern? |
Arnold,
I drew an image of your shroud, extended it to the apex at the top and labeled some points.
I want to determine the distance from A to E, what I have called x inches in the diagram. Triangles ACD and ABE are similar so
x/3 = (18+x)/12
Solving this equation for x gives x = 6 inches. Thus your pattern will be cut from a sector of a circle of radius 18 + 6 = 24 inches.
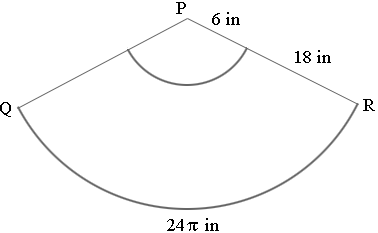
The length of the arc QR is the circumference of the circle at the base of the cone in the first diagram. The circumference of a circle is 2
r and the radius of the circle at the base of the cone is 12 inches so the length of the arc QR is 24 inches.
This arc is a portion of the circumference of the circle with centre P and radius 24 inches. The circumference of this circle is 2 r which is 48 inches. Hence the arc QR is half circumference of the circle and thus the angle RPQ is 180 degrees. So, here is the pattern
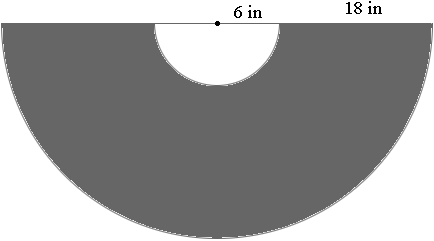
Cut out a semicircle of radius 24 inches and then remove a concentric circle of radius 6 inches.
If you have access to a digital camera, send us a photo of the completed project.
Penny
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.