 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Subject: Exponential form When dealing with imaginary numbers in engineering, I am having trouble getting things into the exponential form. The equation is -1+i now I do know that |
Hi Austin,
To express -1 + i in the form r ei
= r (cos() + i sin()) I think of the geometry. In the complex plane plot the point -1 + i.
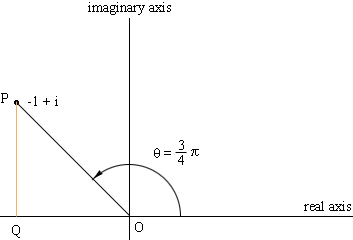
The modulus r of p = -i + i is the distance from O to P. Since PQO is a right triangle Pythagoras theorem tells you that r = √2. The argument of P is the angle, measured counterclockwise from the positive real axis to the line segment OP. Here = 3/4 
. Cos( 3/4 ) = -1/√2 and sin(3/4 ) = 1/√2. Thus
You don't need to use the diagram. The modulus of x + iy is √(x2 + y2) which for -i + i is
r = √((-1)2 + 12) = √2
Also x = r cos () and y = r sin() so -1 = √2 cos () and 1 = √2 sin (). This gives = 3/4 .
Penny
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.