 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Bharathi, a student: given a circle with radius r and a point x,y on its circumference,output two other points x1,y1 and x2,y2 on the circle so that all 3 points form a equilateral triangle. i want a clear explanation please |
Hi Bharathi,
I presume you have the center of the circle (h, k) as well. Here's how I would do this. The gist is to convert it to a polar co-ordinate system, rotate to find the other two points, then convert back to cartesians.
- Apply the transformation x
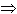x - h and y 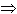y - k to slide the centre to the origin. - Switch to polar coordinates (r, θ) using the relationship θ = tan-1(y/x).
- Apply two 120o angular transformations to find the two other points in polar form (r, θi).
- Convert both new points back to the cartesian coordinates using the relationships xi = r cos(θi) and yi = r sin(θi).
- Apply the transformation xi 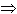xi + h and yi 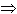yi + k for both points to move the centre back.
Hope this helps,
Stephen La Rocque.
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.