A circle is stretched horizontally by a factor of 2

HOME

Math Central

Quandaries & Queries

Question from bob, a student:

I was wondering if you could double check my work?

the question is as follows:
The circle x^2+y^2-2x-3= 0 is stretched horizontally by a factor of 2
to obtain an ellipse what is the equation of this ellipse in general form?

My work:
(x^2-2x+1)+y^2=4
(x-1)^2+y^2=4
The ellipse will have a horizontal axis of 4 and vertical axis of 2. the
semi-horizontal and semi-vertical axes are (2,1) therefore the equation
is:
(x-1)^2/2^2 + (y^2)/ (1^2) =1
is this correct?

Hi Bob,

I agree with your rewriting of the equation x²+y²-2x-3 = 0 as (x-1)²+y²=4 since then it is clear that the equation represents the circle with centre (1,0) and radius 4. This is the green circle in my diagram.

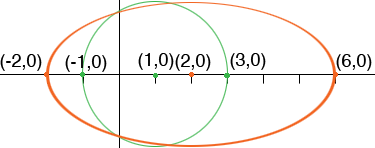
circle and ellipse

If you then stretched horizontally by a factor of 2 you multiply the x-values by 2. Thus the centre of the circle (1,0) moves to (2,0), the point (3,0) moves to (6,0) and the point (-1,0) moves to (-2,0) and I get the orange ellipse.

What is its equation?

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.