| |||
| Math Central | Quandaries & Queries |
|
Question from Brooklyn, a student: Is there a way to find the perimeter of a rectangle if you have the area, or vice versa? If so, what is the equation? |
We have two responses for you
Hi Brooklyn,
Suppose you have 4 feet of picture frame material and you want to make a frame for one of your photos. You could make a frame for your photo of aunt Martha and uncle Fred's new baby.
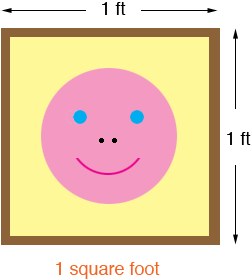
or you might make a frame for a photo of your pet giraffe
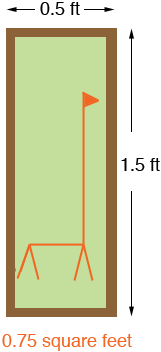
or for a photo you took on your trip to the mountains.
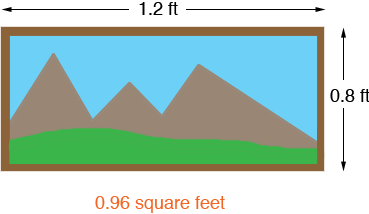
Each of these rectangles has the same perimeter, 4 feet, but the areas are quite different. There is no direct relationship between the perimeter of a rectangle and its area.
Penny
Hi Brooklyn,
Just knowing one piece of information, such as perimeter or area, is simply not enough to determine the exact dimensions of any rectangle. A rectangle of area 20 square units could have dimensions of 2 x 10 or 4 x 5 or 1 x 20, etc. Each of these rectangles has a different perimeter (24 units, 18 units and 42 units respectively).
You would need to know a combination of any two of the following: length, width, perimeter, area.
Obviously, if you know the length and width you're set! You can calculate the perimeter using P=2L +2W and you can calculate the area using A = LW
If you know the area and either length or width, you can use the area formula to determine the other dimension:
Given A = 24, L = 8
W = A/L
W =24/8
W = 3.
Now you know both dimensions and you can determine the perimeter.
If you know the perimeter and either length or width, you can use the perimeter formula to determine the other dimension:
Given P = 40, L = 16
W = P/2 - L
W = 40/2 - 16
W = 20 - 16
W = 4
Now you know both dimensions and you can determine the area.
If you know both the area and the perimeter, you can also determine the dimensions, but it takes a little more work and involves either guessing and checking (which may prove difficult or impossible if any dimension is irrational) or solving a quadratic equation.
Given A = 15, P = 16
15 = LW
16 = 2L + 2W Isolate the W, substitute into the first equation and solve.
16 - 2L = 2W
8 - L = W
15 = L(8 - L)
15= 8L - L2 Move all terms to one side and factor.
L2 - 8L + 15 = 0
(L - 5)(L - 3) = 0
L - 5 = 0 L - 3 = 0
L = 5 L = 3
We would choose L = 5 (only because by convention we think of the length being the longer side) and by substitution into one of our original equations we find the width is 3.
Hope this helps,
Leeanne
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.