 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
What is the area of an equilateral triangle inscribed in a circle whose circumference is 6 pi?? PLEASE HELP |
Hi Caitlin,
The circumference of a circle is 2
r and your circle has a circumference of 6. Thus
6
and therefore r = 3.
In the diagram C is the centre of the circle and M is the midpoint of PQ. The area of the inscribed circle is 3 time the area of triangle PQC.
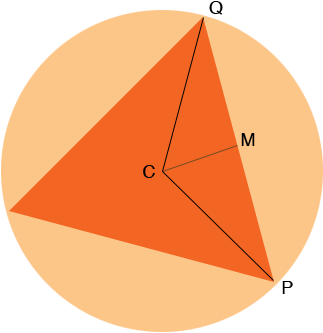
The area of a triangle is half the base times the height and hence the area of triangle PQC is |MQ| 
|MC|.
Since the circle has radius 3, |QC| = 3. Also the inscribed triangle is equilateral and thus each of its angles measures 60 degrees. Thus the measure of angle MQC is 30 degrees and angle CMQ is a right angle so the measure of angle QCM is 60 degrees. Can you now find the lengths |MC| and |MQ|?
Penny
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.