An irregular tetrahedron

HOME

Math Central

Quandaries & Queries

Question from Carrie, a student:

Assume a tetrahedron (not regular) with vertices A, B, C, O, in which vertex A is at (0,0,0) in Cartesian space, line-segment AB is the x-axis, and face ABC defines the x-y plane (but no edge is parallel to the y-axis). Assuming that the xyz coordinates of O are all positive, and given the lengths of all of the line-segments (AB, BC, AC, AO, BO, CO), but none of the angles, what is the formula for calculating the xyz coordinates of O? Thanks much!

Hi Carrie,

I let |BC| = a, |CA| = b and |AB| = c then B bas coordinates (c, 0 , 0). Let C = (r, s, 0) and O = (t, u, v).

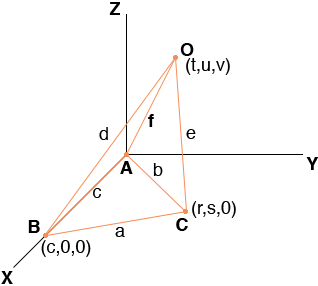
tetrahedron

First I want to find the coordinates of C. The distance from A to C is b and the distance from B to C is a so

r² + s² = b² (1)
(r - c)² + s² = a² (2)

Subtract equation (1) from equation (2) and solve the resulting equation for r. Substitute this value into equation (1) and solve for s.

Now find the coordinates of O. You now know a, b, c, d, e, f, r and s and again using the distance formula

t² + u² + v² = f²                               (3)
(t - c)² + u² + v² = d²                       (4)
(t - r)² + (u - s)² + v² = e²                 (5)

Subtract (3) from (4) and solve for t. Substitute this value into (4) and (5). Subtract (4) from (5) and solve for u. Substitute the values you have for t and u into (3) and solve for v.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.