| |||
| Math Central | Quandaries & Queries |
|
Question from Claire, a parent: Show that the roots of (x - k)(1-3x) + 1 = 0 are real and distinct for all real values of k. Hence, or otherwise, find the range of 9sin^2 r - 6sin r + 13 |
Hi Claire,
I expanded (x - k)(1-3x) + 1 = 0 to obtain a quadratic in x. I then used the general quadratic to solve for x and examined the discriminant, b2 - 4ab. The discriminant is a quadratic in k. The quadratic equation (x - k)(1-3x) + 1 = 0 has distinct real roots of this discriminant is positive.
Try this and see if you can show that the discriminant is positive. If you have trouble write back and tell us what you got for the discriminant and we will try to help.
Harley Weston
Claire wrote back.
Hi Harley
Here are the steps that I managed before getting stuck.
(x-k)(1-3k)+1=0
(x-3x^2-k+3kx+1)=0
3x^2-3kx-x+k-1=0
3x^2-x(3k+1)+(k-1)=0
If the roots are real and distinct then b2-4ac > 0
(3k+1)2 - 4(3)(k-1)
= 9k2-6k+13
I can't factorise it so how do I show that it is positive. Please help.
Thank you.
Regards
Claire
Claire,
That's exactly what I got but you should say
If b2-4ac > 0 then the roots are real and distinct.
I agree 9k2-6k+13 cant be factored so I solved 9k2-6k+13 = 0 using the general quadratic again. This time the discriminant is negative so the roots are not real!
Consider the function
z = 9k2-6k+13
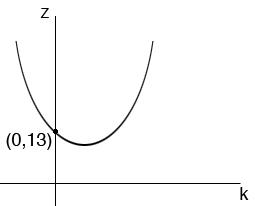
Its graph in the kz-plane never crosses the k-axis since 9k2-6k+13 = 0 has no real solution. When k = 0 the value of z is 13 which is positive. Hence 9k2-6k+13 is positive for some value of k and to become negative it would have to cross the k-axis, which it doesn't. Hence 9k2-6k+13 is positive for all values of k.
The graph of z = 9k2-6k+13 looks something like
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.