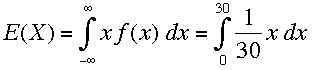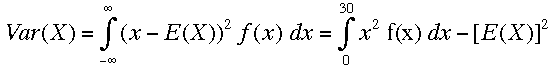| |||
| Math Central | Quandaries & Queries |
|
Question from Claudia, a student: A particular employee arrives to work some time between 8:00 am - 8:30 am. Based on past experience the Company has determined that the employee is equally likely to arrive at any time between 8:00 am - 8:30 am. On average, what time does the employee arrive? What is the standard deviation of the time at which the employee arrives? Find the probability that the employee arrives exactly at 8:12 am? Find the probability that the employee arrives between 8:20 am - 8:25 am? |
Hi Claudia,
I let the random variable X be the time after 8:00 in minutes. Thus 0 ≤ X ≤ 30. Sine the employee is equally likely to arrive at any time X the probability density function f(x) is the uniform distribution so f(x) = 1/30.
The first question is asking for the mean of this distribution, that is the average time the employee arrives after 8:00 is
The standard deviation is the square root of the variance Var(X) where
Can you see how to complete the problem?
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.