Hi Dani,

Start with an equilateral triangle ABC with each side of length h. With the vertex A as centre, draw an arc of the circle of radius h that passes through the other two vertices. Repeat this construction at the vertices B and C. The resulting plane figure ABC is the Reuleaux Triangle of width h.

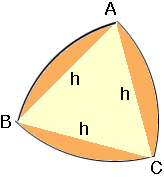
Consider he plane figure bounded by the line segments AB and CA and the arc BC. This is a sector of a circle with centre A, radius h and centre angle 60 degrees or /3 radians. Thus the area of this sector is

1/2 h² /3 or 1/6 h²

The similar sectors with centres B and C each have the same area and hence the sum of these three areas is

3(1/6 h² ) = 1/2 h²

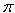
Looking back at the diagram you can see that this calculation included the equilateral triangle ABC three times and hence the area of the Reuleaux Triangle ABC is

1/2 h² - twice the area of the equilateral triangle ABC.

Find the area of the equilateral triangle and simplify this expression. Compare this area to the area of the circle of width h. The circle of width h has radius h/2 and hence its area is

h²/4

I hope this helps,
Penny