Hi Daniel,

I let r = D/2 be the radius of the circle and drew a diagram.

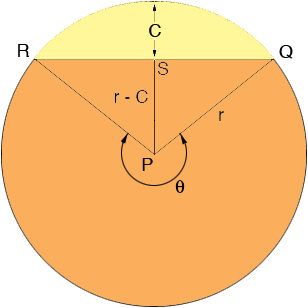
I am going to find the area of the part of the circle that remains after you cut off the yellow piece as the sum of the area of the triangle QRP and the area of the large sector PRQ, going counterclockwise from R to Q.

S is the midpoint of the line segment RQ and angle QSP is a right angle so by Pythagoras' theorem

r² = (r - C)² + |QS|²

The area of a triangle is half the base times the height so the area of triangle QRP is

|QS| (r - C) = Sqrt(r² - (r - C)²) (r - C)

where Sqrt is the square root.

The area of the sector PRQ is 1/2 r² where is the angle in the diagram, measured in radians. To find the angle I again look at triangle QSP. The cosine of the angle SPQ is (r - C)/r and hence

angle SPQ = cos^-1((r - C)/r)

and thus

= 2 - 2 cos^-1((r - C)/r)

Now you can use this value of to find the 1/2 r² , the area of the sector PRQ.

When using the cos^-1 function on your calculator make sure it is returning a value in radians not in degrees.

Penny