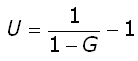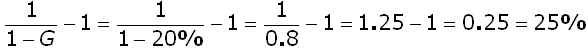We have two responses for you

Drew,

Both methods are used but in my opinion when you say you have a 20% markup most people will assume you used the first method. In this case you are calculating 20% of your cost (0.20 × $938.00 = $187.60) and adding it to your cost ($938.00 + $187.60 = $1125.60) to obtain the "sticker price". Thus the markup ($187.60) is 20% of your cost.

In the second method 20% of $1172.50 is $234.50 and if you add $234.50 to your cost of $938.00 you arrive at $1172.50. Thus the markup ($234.50) is 20% of the sticker price.

Harley

Drew,

The Markup percentage is the percentage of the selling price not represented in the cost of the goods. So if the markup is 20%, then 80% of the selling price is the cost. Your cost is $938, so the $938/80% = $1172.50 would be the cost for a product with a 20% markup.

The contrasts with the gross Margin percentage, which is the percentage by which you increase the cost in order to find the selling price. If the margin were 20%, then you would calculate $938 * 120% = $1125.60 as the selling price.

Thus the Margin is the view from the manufacturing side of things and the Markup is the view from the sales side of things. The Margin is always lower and you can relate the two using this equation, where U
is the markUp as a decimal (20% = 0.20) and G is the marGin as a decimal:

So for instance, if you knew you wanted a 20% margin, you could find
the related markup:

So a margin of 20% is a markup of 25%. (Conversely, a markup of 20% is a margin of 16 2/3%.)

Hope this helps,
Stephen La Rocque.