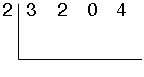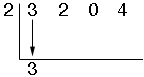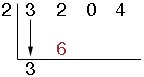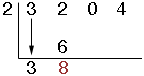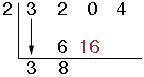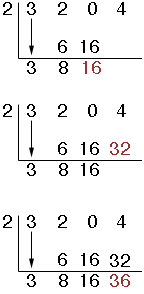Hi Edward,

Synthetic division is a method of dividing polynomials.
When given 3x³ + 2x² + 4 divided by x-2, you first must solve for x.

So set x-2=0, then x=2

To use this with synthetic division, we must take the coefficients in the polynomial and make sure all powers of x are accounted for. So, 3x³ + 2x² + 0x¹ + 4 (notice there was no coefficient for x¹, so we use 0 as a place holder).

Then we are ready to use synthetic division. The x value goes on the outside the box and the polynomial coefficients inside.

We bring the first number down,

then multiply it by our divisor (3 2 = 6) and place this value under our next coefficient.

Add these 2 numbers (2+6=8). The answer is placed vertically below

and used as our next number to be multiplied by the divisor (8 2 = 16),

continue this process 'till you run out of coefficients.

The number left over in the bottom right corner is your remainder. The numbers to the left of this are your quotient. (remember we are going down by one power)

ie. (3x³ + 2x² + 4) (x - 2) = 3x² + 8x¹ + 16 remainder: 36

Hope this helps.
Melanie