| |||
| Math Central | Quandaries & Queries |
|
Question from fhay, a student: A ship leaves a port and sails for 4 hours on a course of 78 degrees at 18 knots. Then the ship changes its course to 168 degrees and sails for 6 hours at 16 knots. After 10 hours(a) what is the distance of the ship from a port and (b) what is the bearing from the port to the ship? |
Fhay,
I am going to interpret your bearing measurements as degrees East of North which I think is the aviation convention in the northern hemisphere. Hence I have the following diagram.
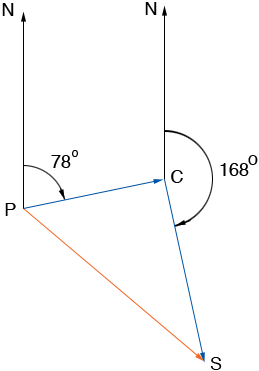
P is the port, C is the point where the change of direction is made and S is the position of the ship after 10 hours. On the first leg of the trip the ship travels 18 knots for 4 hours and hence the length of PC is 4 × 18 = 72 nautical miles. Similarly the length of CS is 96 nautical miles.
Since the angle NPC measures 78 degrees, the angle PCN measures 102 degrees and thus the angle SCP measures 90 degrees. Hence you can use Pythagoras' Theorem to find the distance from P to S. Again since angle SCP measures 90 degrees the tangent of the angle CPS is |SC|/|CP| = 72/96 = 3/4. Hence you can find the measure of the angle CPS and thus the bearing of S from P.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.