 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Gilligan, a student: NOTE: This question is about NUMERICAL/STATISTICAL data. A species of beetle has a 3yr life span. Half the females in their first year will survive into the second year the rate from second to 3rd year is 1/3. Each female breeds in the 3rd year of life, producing 6 females and 1 male. No females survive beyond the 3rd year. Let xsub1, xsub2, xsub3 denote the number of females in the 1st, 2nd and 3rd year. (a) What will be the number of females in the 1st, 2nd and 3rd years of life next year? (b)Show that the numbers in each group will return to the same values every 3 years? (c) Given a total of 3600 beetles, over the 3 age groups, calculate the number in each group? My Work Done: Not sure what type of calculations to use and whether it is a recurrence a) I have as answer for 1st part as: this year- xsub1=1, xsub2= 1/2*xsub1, xsub3= 1/3*xsub2 Next year:- xsub1=(last years) xsub3*6; xsub2= 1/2*xsub1; xsub3=1/3*xsub2 What am I doing wrong? |
Hi Gilligan,
I think what you are to do is
- Number in year 1 is x1
- Number in year 2 is x2 = 1/2
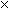x1 - Number in year 3 is x3 = 1/3 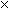x2 = 1/3 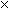(1/2 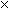x1) = 1/6 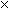x1
Each female in year 3 produces 6 female offspring so at the end of year 3 is
6
Penny
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.