You can tell we liked this problem. You have three responses.

Hi,

If you know the measure, t degrees, of each interior angle then each exterior angle has measure
180 - t degrees. Imagine that you start in the middle of one side and walk around the polygon in a counterclockwise direction. Each time you reach a vertex you must turn through 180 - t degrees. When you arrive at the point where you started you have made one complete revolution, that is you have turned through a total of 360 degrees. How many times did you turn?

Penny

Hi there.

The sum of the exterior angles of any convex polygon is 360 degrees. That means that if you have n sides, then each exterior angle of a regular polygon is 360/n.

If you can find out how the exterior angle is related to the interior angle, you can finish the solution.

Stephen La Rocque.>

Hi,

While it could be done, with algebra, using interior angle sums etc. I would suggest it is easier to understand using exterior angles.

The key fact is that the sum of the exterior angles of a convex polygon is 360 degrees - period!
(IMagine walking around a polygon, turning the exterior angle at each corner. When you finish, you have done one full turn - so 360 degrees. It is also obvious if you 'scan back' from the polygon and look at the edges extended in the direction of a single walk. Again, you see a full circle - see the diagrams below.

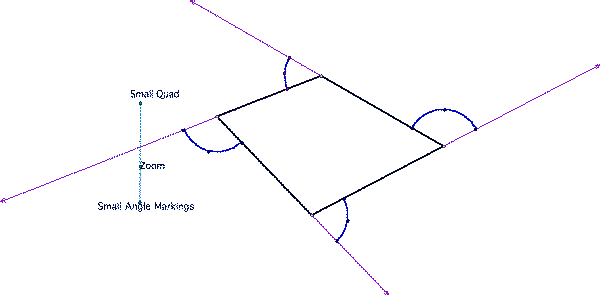
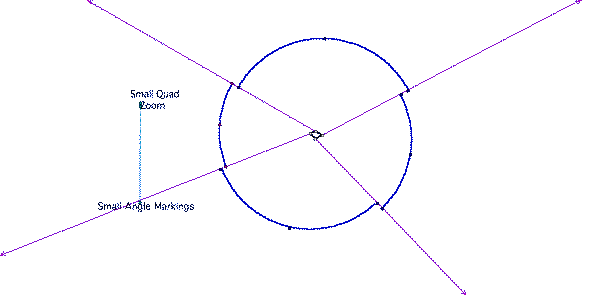
Walter