Golaan,

I drew a diagram (not to scale) of the situation you described. You are interested in the angle of incline, the angle at C, or the grade of the slope from C to A.

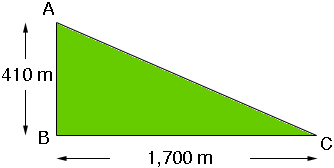
The crucial number here is the ratio of the length of AB to the length BC. In the example you sent this is

410/1700 = 0.241

This is the slope of the incline. The grade is the same as the slope but usually presented as a percentage. The grade here is 0.241 100 = 24.1%.

If you want the measure of the angle at C in degrees you are going to need trigonometry. The ratio of the length of AB to the length of BC is the tangent of the angle at C. In fact you need the inverse tangent, you know the ratio and you want the angle. The inverse tangent is probably a function on your calculator. It may be called tan^-1, or arctan or Atan. You also need to ensure that your calculator is operating in degrees. Sometimes angles are measured in radians and you don't want that.

Using the calculator on my computer I divided 410 by 1700 to get 0.241176... I then pushed the tan^-1 button which gave 13.6... so the angle at C is 13.6 degrees.

I hope this helps. Let us know if we can be of further assistance.

Penny