A rotated rectangle - Math Central

HOME

Math Central

Quandaries & Queries

Question from Graham:

There is a circle inside which from the centre to the top is a rectangle. Size is unimportant.
If I the rectangle is at 0 degrees and I know the co-ordinates of the 4 corners I can do a check to see
whether a given point x,y is inside the rectangle or not.

Question : If the rectangle is rotated by 50 degrees how do I check then as the lines of the rectangle are not perfectly straight with regards to x and y ie at 0 degrees x changes but y is constant and vice versa.
At 50 degrees x and y change together.

Many thanks
Graham

Hi Graham,

Angles are usually measured in a counterclockwise directionso I am going to assume that the rectangle is rotated 50 degrees counterclockwise around the centre of the circle wich is also the origin. Here are my diagrams of the rectangle and the rotated rectangle.

original rectangle

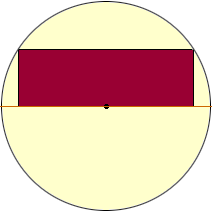
original position

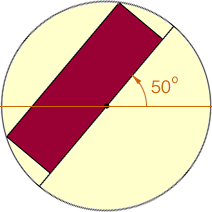
rotated rectangle

rotated 50^o

You now have a point (x, y) in the plane and you want to check to see if it is inside the rotated rectangle. I would take the point (x, y), rotate it 50 degrees clockwise around the centre of the circle and then check to see if the resulting point is inside the original rectangle.

Suppose that you have a point (x, y) in the plane and and you want to rotate it degrees counterclockwise around the origin to arrive at a new point (x', y') then the relationship between (x, y) and (x', y') is

x' = x cos() - y sin()
y' = y cos() + x sin()

In your situation you want to rotate the point 50^o clockwise so = - 50^o. Start with the point in question, (x, y), transform it to (x', y') by

x' = x cos(-50^o) - y sin(-50^o)
y' = y cos(-50^o) + x sin(-50^o)

and check to see if (x', y') is in the original rectangle.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.