Hi Helen,

I tool the diagram you sent and labeled some points.

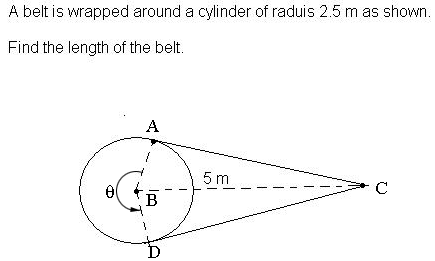
The belt comes off the pulley at the point A and makes a right angle CAB. Thus triangle ABC is a right triangle. You know the lengths of AB and BC so you can use Pythagoras' theorem to find the length of AC which is the same as the length of CD.

The remaining part of the belt is the arc of the circle starting at A and extending counterclockwise around the circle to D. The length a of an arc is given by a = r where r is the radius of the circle and is the angle measured in radians. All that remains is to find the value of .

Penny