| |||
| Math Central | Quandaries & Queries |
|
Question from Irene, a student: How the graph of a parabola f(x)=1/4(x+3)squared-4 can be obtained from the graph of y=xsquared, using Translations and Scaling. |
Hi Irene,
Warning: My diagrams are not to scale and the curves is not a parabolas.
The graph of y = x 2 is a parabola that opens upwards. The vertex of this parabola is at the point where x = 0.
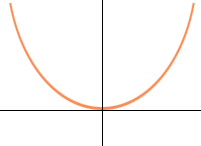
y = x2
If you change x to x - 5 so the equation is y = (x - 5)2 then the vertex is at the point where x - 5 = 0, that is at x = 5. Thus a change from x to x - 5 is a translation of 5 units to the right.
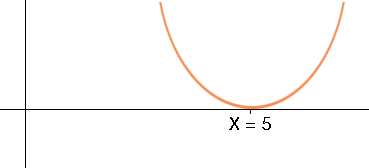
y = (x - 5)2
Now multiple (x - 5)2 by 3. This is a scale factor of 3 in the y-direction. For example when x = 6, (x - 5)2 has a value of 1 but 3(x - 5)2 has a value of 3, and when x has a value of 7, (x - 5)2 has a value of 4 but 3(x - 5)2 has a value of 12. Hence the two arms of the parabola are stretched upwards.
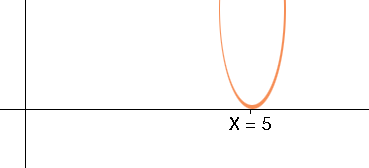
y = 3 (x - 5)2
Finally add 2 to the right side. This adds 2 to the y-value of each point and has the effect of translating the curve 2 units upward, in the y-direction.
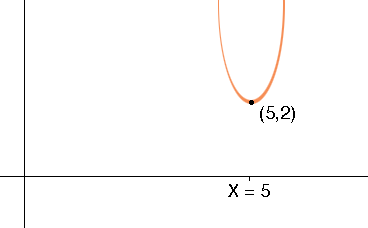
y = 3 (x - 5)2 + 2
Now try this procedure with your expression,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.