A square contains five circles with the same radius.- Math Central

HOME

Math Central

Quandaries & Queries

Question from Jamie, a student:

Your help on this question will be much appreciated.

A square has a side length on 1 m.
The square contains five circles with the same radius.
The centre of one circle is at the centre of the square and it touches the other four circles.
Each of the other four circles touches two sides of the square and the center circle.
Find the radius.

Thank you!

Hi Jamie.

I drew a diagram of half of the square and labeled some points.

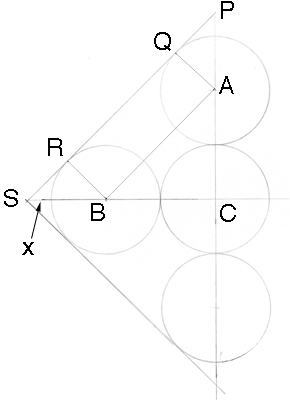
half the square

Let r be the radius of the circles and x the distance from S vertex to the circle.

ABC is a right triangle and |BC| = |CA| = 2r so from Pythagoras' theorem |AB| = 2√2r. Thus |QR| = 2√2r and hence
|RS| = (1 - 2√2r)/2. Triangle RSB is a right triangle and hence by Pythagoras' theorem again

|BR|² + |RS|² = |SB|²

Hence

r² + (1 - 2√2r)²/4 = (r + x)² (1)

Triangle PSC is a right triangle and hence

(3r + x)² + (3r + x)² = 1²

x = (1/√2) -3r

Substitute this value for x into equation (1), simplify to obtain a quadratic in r and solve. You will obtain two values for r so make sure you choose the correct one.

Hope this helps,
Penny.

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.