| |||
| Math Central | Quandaries & Queries |
|
Question from janine, a student: A trough is formed by nailing together, edge to edge, two boards 11 ft. in length, so that the right section is a right triangle. If a 15 gallon of water are poured into the trough and if the trough is held level so that a right section of water is an isosceles right triangle, how deep is the water? (231cu.in=1 gal.) |
Hi JaninI hope there are ends on this trough, otherwise all the water will run out.
The volume of water in the trough is 15 gallons or 15 × 321 = 3465 cubic inches. The length of the trough is 11 × 12 = 132 inches and the volume of the water is the area of the triangular cross-section times the length so the area of the triangular cross-section is
3465/132 = 26.25 square inches.
I drew a diagram of the triangular cross-section of the trough.
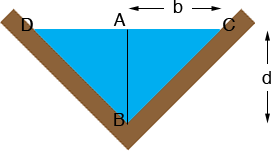
The area of the triangular cross-section of the water is b × d so
b × d = 26.25 square inches.
The triangle DCB is an isosceles right triangle so the measure of the angle BCD is 45 degrees. The triangle ABC is also a right triangle and hence, since the measure of the angle BCA is 45 degrees triangle ABC is isosceles also. What does that tell you about b and d?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.