| |||
| Math Central | Quandaries & Queries |
|
Question from Jemina, a student: John ate 1/4 of a cake, Maria ate 1/4 of the remaining cake. What was the unit or whole in John's case? In Maria's case? How much of a full pan was there in each case? |
Jemima, we have two responses for you:
I baked the cake in a square pan. John cut it into quarters and ate one of them leaving three quarters of the cake.

Maria wants one quarter of what is left and she sees how to cut what John has left into twelve equal size pieces.

Thus if she takes three of these pieces she will have one quarter of what john left.
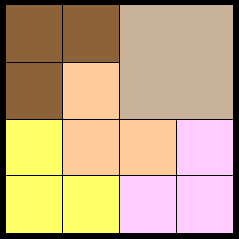
Now I see what I should have done in the first place. I should have cut the cake into sixteen equal size pieces.

John could take four of these pieces and Maria could take three of them.
This is certainly not the most efficient way to approach this problem but hopefully it helps you understand the efficient way of using fractions.
John eats 1/4 of the cake. Maria then wants 1/4 of the 3/4 of a cake that is left.
1/4 of 3/4 is 1/4 × 3/4 = 3/16
so Maria takes three-sixteenths of the cake.
I hope this helps,
Penny
Hi Jemima.
I will solve a similar question so you can see how to solve this one.
Sue used the computer for 1/3 of the day. Her sister Penny used the computer for 1/2 the remainder of the day. What was the unit or whole in each case? How much of a full day was left in each case?
A "unit" is one. Like the related words "unity", "unison", "uniform", "unitary" - they all refer to the whole so this is a question about grammar. In the question, what is the whole that we are taking a fraction of?
In Sue's case, we are taking 1/3 of the day. So the unit or whole in Sue's case is 1 day.
In Penny's case, we are taking 1/2 of the remainder of the day. But was is the remainder of the day if Sue took 1/3 of the day? It is equal to the original unit (1 day) minus Sue's time (1/3 of a day). And that is 2/3 of a day. So the "unit" or "whole" in Penny's case is 2/3 of a day.
How much was left in Sue's case? We already learned that: it is 1 - 1/3 = 2/3 of a day.
How much was left in Penny's case? She started with 2/3 of a day available to her and took half of that. So she took 1/2 of 2/3 of a day. That is 1/2 × 2/3 which equals 2/6 (to multiply fractions you multiply the tops and the bottoms separately). Then simplifying this, we see that 2 goes into both the top and the bottom, so 2/6 = 1/3. Thus Penny used 1/3 of the day. Since she started with 2/3 and used 1/3, then 1/3 of a day is left over.
Have a great weekend,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.