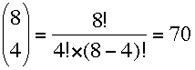Hi Joe,

In your "12 separate numbers" you have eight distinct digits and the number of ways of choosing four digits from eight digits is

Penny

I see that it has been answered. But PENNY NOM assumed I did not want to include the duplicate numbers. She cut it down to 8 instead of the 12. Can someone redo the math on this using all 12, including dupes, numbers.

Thanks,
Joe

Well I'm not sure it makes sense to use all 12 numbers - for example, do you want to allow 3939 and 3399? Is the problem is to create a 4 digit number from a 0, a 1, a 4, a 6, an 8, two 7's, two 9's and three 3's? In this case I think one has to consider quite a number of cases involving how often multiple digits are used. I can slog through that but I'd really like to know exactly what you want first.

Thi direction is correct. I would want 3939, 3399, 9933, 9393, etc. All 4 digits combos of the 12 numbers.

And yes to this question if it makes it clearer: Is the problem is to create a 4 digit number from a 0, a 1, a 4, a 6, an 8, two 7's, two 9's and three 3's?

One has to consider cases:

1. 3 3's are used: there are 4 ways to place the 3 3's in the 4
   spots; for each of those we need to place one of the remaining 7
   distinct numbers in the empty spot. A total of 4x7 = 28 ways.
   
   
2. 2 3's are used: there are 6 ways to place the 2 3's in the 4 spots;
   for each of those we need to place two of the remaining numbers in the
   empty spots. This time however we may use 2 7's or 2 9's, or 2 of the
   remaining 7 distinct numbers to fill in the empty spots. A total of
   6x2 + 6x7x6 = 264 ways.
   
   
3. 1 3 is used: there are 4 ways to place the 3 in the 4 spots; for
   each of those we need to place 3 of the remaining numbers in the empty
   spots. This time however we may use 2 7's or 2 9's and a 3rd digit, or
   3 of the remaining 7 distinct numbers to fill in the empty spots. If
   we use 2 7's (or 2 9's) we can place them in 3 ways and then we need
   to pick one of the remaining 6 distinct numbers to go in the 4th spot.
   This gives 4x2x3x6 = 144 ways. If we use 3 distinct numbers there are
   4x7x6x5 = 840 ways. A total of 984 ways.
   
   
4. 0 3's are used:
   1. 2 9's are used: these can be placed in 6 ways; if the 2 7's are
      used to fill in the other two spots this can only be done in 1 way,
      otherwise we need to fill in the 2 spots with 2 of the 6 distinct
      remaining numbers (remember we can't use 3 here as we're doing 0 3's).
      The number of ways is 6x1 + 6x6x5 = 186 ways.
      
      
   2. 2 9's are not used but 2 7's are used: these can be placed in 6
      ways; we need to fill in the other 2 spots with 2 of the 6 distinct
      remaining numbers (remember we can't use 3 here as we're doing 0 3's).
      The number of ways is 6x6x5 = 180 ways.
      
      
   3. Neither 2 7's nor 2 9's are used: Then we have to place 4 distinct
      numbers from the 7 allowed into the 4 spots, a total of 7x6x5x4 = 840
      ways.
      

In total we have 28 + 264 + 984 + 186 + 180 + 840 = 2482 ways.

Penny