| |||
| Math Central | Quandaries & Queries |
|
Subject: development of cylinder think of a tube,say 50mm in diameter made out of cardboard, project vertical lines at right angles from the base at say every 2mm right round the tube in pencil.No pretend you can put this cardboard tube in a saw and cut it at 45degrees. Get a pair of scissors and cut it at the lowest end and lay it out flat.It now looks like a graph,how do you work out each of these vertical lengths possibly chord lengths |
Hi John.
Not only does it look like a graph, it looks like a perfect graph of -cos(x) !
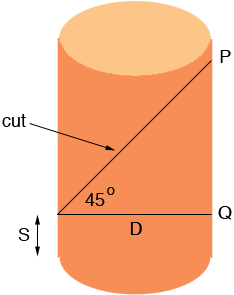
In our diagram D is the diameter of the tube and since the cut is at 45 degrees the length of PQ is also D and thus the amplitude of the cosine function is D/2 = R, the radius of the tube. The number of cycles is exactly one (once around the tube). If N is the line number from the left hand side, then
the angle x is just 360 degrees
horizontal spacing
N / circumference.
And lastly, the vertical shift depends on where you cut: it is the length from the bottom of the tube to the bottom of the cut (S) plus the amplitude.
So L(N) = S - Rcos(360HN/C)
where L(N) is the length of line number N, H is the horizontal spacing, C is the circumference.
Hope this helps,
Stephen and Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.