Hi Katrina,

I pasted in the graphic you sent

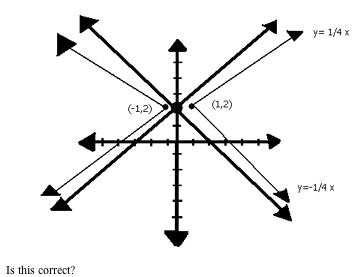
You have the asymptotes intersecting at (0,2) which is correct but I am not sure you have the slopes correct. To find the asymptotes, look at the equation in general form which you have

(y-2)² – x²/4 =1

Set the right side to zero and factor the left side as a difference of squares

(y - 2 - x/2)(y - 2 + x/2) = 0

This is then two equations

y = x/2 + 2 and
y = -x/2 + 2.

These are the equations of the asymptotes.

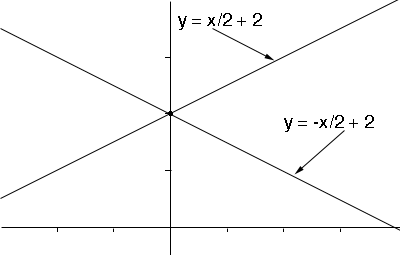
Now you know the graph of the hyperbola lies in either the region of the plane shaded orange below or the region of the plane shaded green. To determine where the graph lies you just need to plot one point.

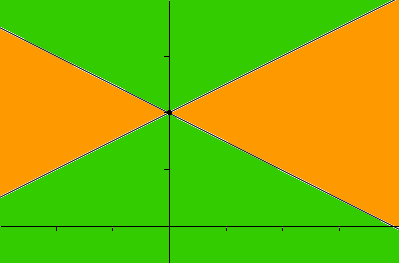
The equation is

(y-2)² – x²/4 =1

It looks like y = 2 is an easy value to substitute into the equation as it makes the first term zero, but that gives

- x²/4 =1 or x² = -1

which is impossible, so there is no point on the graph with y-coordinate equal to 2.

A second easy value to substitute is x = 0 as this makes the second term zero and gives

(y-2)² =1 or y - 2 = ±1

which gives the points (0, 1) and (0, 3)

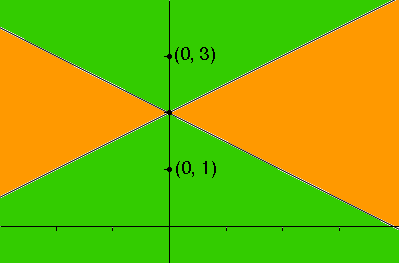
Hence the hyperbola lies in the portion of the plane shaded green.

I hope this helps,
Penny