Hi Kevin,

I drew a cross section of the culvert (not to scale) to make sure that I have the correct picture.

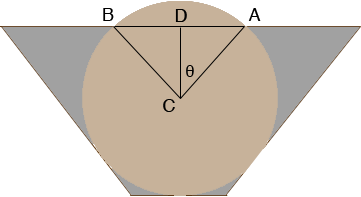
The volume of the irrigation ditch is the area of the trapezoidal cross section times the length. The area of a trapezoid is the average of the lengths of the parallel sides times the distance between the parallel sides so the area of the trapezoid is

(40 + 12)/2 × 16 = 416 square inches

The ditch is 20 feet = 20 × 12 = 240 inches long so the volume of the ditch is

416 × 240 = 99840 cubic inches.

You need to subtract from this the volume displaced by the culvert. The volume of the ditch displaced by the culvert is also the area of the cross section time the length. This time the cross sectional area is the area of the circle in the diagram minus the cap above the line segment AB since the culvert sits 2 inches above the top of the ditch. The area of a circle is π r² where r is the radius of the circle so in your case the area of the circle is

π × 9² = 254.47 square inches.

I am going to find the area of the cap above the line segment AB by calculating the area of the sector ABC and subtracting the area of the triangle ABC. In the diagram |CA| = 9 inches and |CD| = 9 - 2 = 7 inches so

cos(θ) = 7/9 and hence θ = cos^-1(7/9) = 38.94 degrees.

Thus the measure of the angle BCA is 2 × 38.94 = 77.88 degrees. The area of the sector ABC is a fraction of the area of the circle, in fact this fraction is 77.88/360 = 0.2163. Thus the area of the sector is

0.2163 × 254.47 = 55.05 square inches.

Also from the diagram sin(θ) = |AD|/9 so

|AD| = 9 × sin(38.94) = 5.66 inches.

Thus the area of the triangle ABC is

1/2 × base × height = 1/2 × (2 × 5.66) × 7 = 39.60 square inches.

Finally the area of the cap above the line segment AB is

55.05 - 39.60 = 15.45 square inches

and hence the area of the circle minus the area of the cap is

254.47 - 15.45 = 239.02 square inches

and the volume of the ditch displaced by the culvert is

239.02 × (20 × 12) = 57364.8 cubic inches.

Hence the volume of concrete needed is

99840 - 57364.8 = 42475.2 cubic inches.

There are 36 × 36 × 36 = 46656 cubic inches in a cubic yard so you need

42475.2/46656 = 0.91 yards of concrete.

Penny