the Golden Gate bridge- Math Central

HOME

Math Central

Quandaries & Queries

Question from Khan, a student:

Hi,

I am doing a project on parabola and Bridges. I have chosen the Golden Gate bridge as my bridge. Now The suspension cables are shaped like a parabola.

We have to derive an equation for this parabola. We have to assume the vertex is (0,0). Now I am having troubles writing the equation in standard form.

The information is this
Height of tower above water:
746 ft = 227 m

Height of tower above roadway:
500 ft = 152 m

Length of one side span: 1,125 ft = 343 m

length of suspension span including main span and side spans: 1.2 miles = 6,450 ft

Now my question is this, i KNOW THE standard form for this parabola opening up would
be (x-h)squared = 4a (y-k)

Since h,k are 0,0 the equation will now take the form of xsquared = 4ay
My question is to find the equation I need to know A how do i get this a based on the above
provided info. Thanks for your help and concern.

Khan,

I put the important information on a diagram.

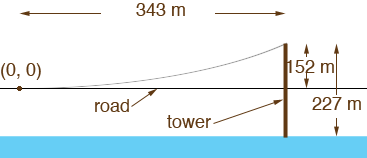
bridge

Since the vertex of the parabola (0, 0) is on the roadway at the centre of the span the point at the top of the tower has coordinates (343, 152). Thus the point (343, 152) is on the curve so substitute the coordinates of this point into x² = 4ay and solve for a.

Actually the cables in a suspension bridge do not have a parabolic shape but the curve is very close to a parabola. It is a curve called a catenary.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.