The question is whether the games is fair or unfair?

HOME

Math Central

Quandaries & Queries

Question from kk, a student:

Players have two red chips each with an A side and a B side, and one blue chip with an A side and a B side.
The players flip all three chips. Player one wins if both red chips show A, if the blue chip shows A, or if all chips show A.
Otherwise player two wins. The Question is: Whether the games is fair or unfair and to draw a probability tree to show the answer.
Hope you can help

Hi kk,

A probability tree shows every possible outcome of the the chip toss. The first red chip will show either an A or a B (so far 2 different outcomes). For each of those outcomes, the second red chip can also either be an A or a B (so now we're up to 4 different outcomes: AA, AB, BA, BB). For each of the four possible outcomes on the first two chips, we also have that the blue chip can be either A or B. So there are 8 possible outcomes in total, as shown by the 8 branches in this tree:

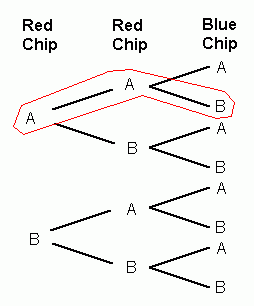
probability tree

Each branch in the tree shows one of the possible results of the chip toss. For example, the branch I have circled shows the result when the first red chip is an A, the second red chip is an A, and the blue chip is a B. In this case, player 1 would win. How many other branches give a win for player 1? How many branches result in player 2 winning? Can you take it from here?

Haley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.