Hi Kyrie.

If both give the same value for f, then the f values equal each other.
Two things that both equal a third thing have to equal each other, so
9c / 5 + 32 = 2c + 30

Solve for c.

Stephen La Rocque.>

Kyrie wrote me back saying:

hi sue
ref my question you answered yesterday on temperature ?
f = 9c / 5 + 32
f = 2c + 30
your ans was   9c / 5 + 32 = 2c + 30 solve c
is c =  -1.428   if so, temp of f are not equal ? i'm confused ?

Hi Kyrie.

That's right. The two equations are giving you two different values for f for a given value c.

Look at your two equations. They are linear equations (that means when you graph them, each one forms a line). In the spot where the two lines cross, they give the same value of f for a particular value of c. Let's graph them with f as the vertical axis (replaces the usual y axis) and c as the horizontal axis (replaces the usual x axis):

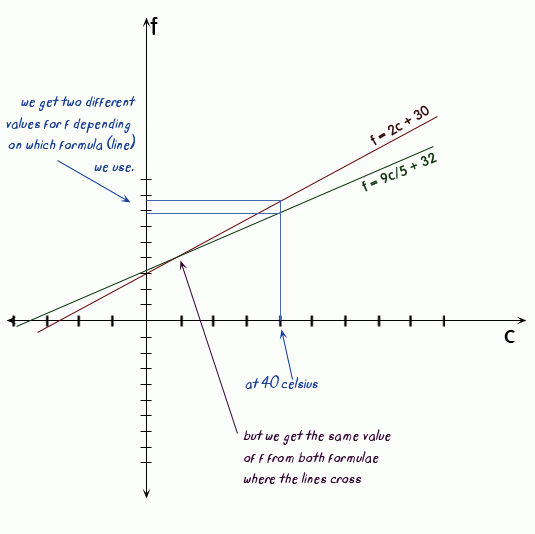
So when you solve for c, you are solving for that point of intersection where the two values of f are the same.

9c/5 + 32 = 2c + 30
c/5 = 2
c = 10.

So this tells us that when c is 10 celsius, both formulae give the same value for f. Let's check:

f = 9(10)/5 + 32
f = 18 + 32 = 50.

f = 2(10) + 30
f = 20 + 30 = 50.

Yes this checks out.

If you try it for -1.428, you will find that they give different values, so that is not the answer.

Hope this graph helps you to understand how it works, Kyrie.
Stephen La Rocque.