A probability problem - Math Central

HOME

Math Central

Quandaries & Queries

Question from Lina, a student:

A point P is selected at random from the interior of the pentagon with vertices
A = (0,2), B = (4,0), C = (2 π +1,0), D = (2 π +1,4), and E = (0,4). What is the probability
that <APB is obtuse?
A. 1/5
B. 1/4
C. 5/16
D. 3/8
E. 1/2

Hi Lina.

The only way for APB to be obtuse is for it to be lower than A and to the left of B.

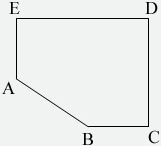
pentagon

Since P is inside the pentagon it is within the area of the pentagon. The chance that it is obtuse is the ratio of the area of the right triangle (below A, left of B and above the line AB) to the area of the whole pentagon.

So find the areas of the pentagon and this triangle and you'll have solved the problem.

When we solved it we didn't get one of the possible choices. Are you sure that you have the correct ccordinates for C and D?

Hope this helps,
Stephen and Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.