| |||
| Math Central | Quandaries & Queries |
|
Question from Lindsay, a student: Hello. I'm trying to a math problem and have searched the internet for equations, but have come up empty handed. If you could help, that would be greatly appreciated! |
We have three responses for you
Hi Lindsay,
As in my suggestion for your last problem, I would draw a diagram and label some points.
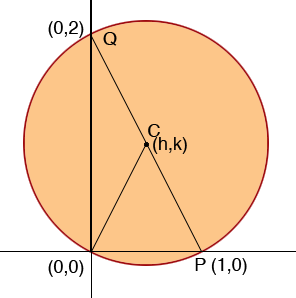
I let the centre of the circle have coordinates (h, k). Suppose the radius of the circle is r. Use the distance formula to write the distance from C to the origin, from C to P and from C to Q. Each of these distances is r so this gives you three equations in the unknowns h, k and r. Solve for h, k and r.
Penny
Hi Lindsay.
We know that any three points (as long as they aren't on a single line) define a circle, so when we mark these coordinates on a graph, we can draw the circle:
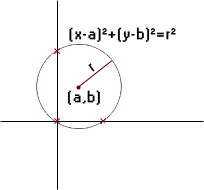 The equation of any circle is (x-a)2+(y-b)2=r2, where (a,b) is the center and r is the radius.
The equation of any circle is (x-a)2+(y-b)2=r2, where (a,b) is the center and r is the radius.
You have three values for (x, y) on the circumference of the circle, so that can create three equations with three unknown values (a, b, and r):
| (0-a)2+(0-b)2 = r2 | (1) | |
| (1-a)2+(0-b)2 = r2 | (2) | |
| (0-a)2+(2-b)2 = r2 | (3) |
So three equations with three unknown values can be solved in the same way as simultaneous equations are normally solved: with the substitution and/or the elimination methods. Solving equations (1) and (2) for b2 gives us:
| r2 - a2 = r2 - (1-a)2 | (4) |
from which you can eliminate r2 from both sides and find a. Once you know a, you can find b and r the same way. Then you will be able to put your values of a, b and r into the equation of the circle(x-a)2+(y-b)2=r2.
Cheers,
Stephen La Rocque.
Lindsay,
I thought of an even easier way to solve this problem.
The center of the circle has to be halfway between the y intercepts and halfway between the x intercepts. That immediately tells you the coordinates of the center. Then you can use the distance formula to any of the three intercepts (the origin would be easiest) to find the radius.
The method I used (and which Penny uses) will work for any three points, not just intercepts, so it is more powerful, but this shortcut works for intercepts.
Stephen.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.