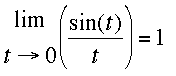Lo,

You didn't ask a question but I expect that you have to find the limit of tan(2x)/sin(3x) as x goes to zero. What you need to know to solve this problem is that

For the moment consider the numerator and denominator of you expression separately. For the denominator, sin(3x) write

sin(3x) = 3x sin(3x)/3x

and notice that as x approaches zero, 3x also approaches zero so sin(3x)/3x will approach 1.

Now look at the numerator and write

tan(2x) = sin(2x)/cos(2x) = 2x (sin(2x)/2x) (1/cos(2x))

and notice again that as x approaches zero, so does 2x and hence sin(2x)/2x approaches 1.

Now you are ready to approach the problem. In the expression tan(2x)/sin(3x) write the numerator and denominator as I showed you, simplify what you can and then take the limit as x approaches zero.

Penny