The volume of a cylinder is

V = r² h             (1)

where r is its radius and h is its height. You need to differentiate this expression and then use what you know about calculus to find the values of r and h that maximize the volume. The challenge is that V is a function of two variables, r and h and you need to express V as a function of one variable to differentiate it. You need to use that fact that the cylinder is inside a sphere to eliminate one variable.

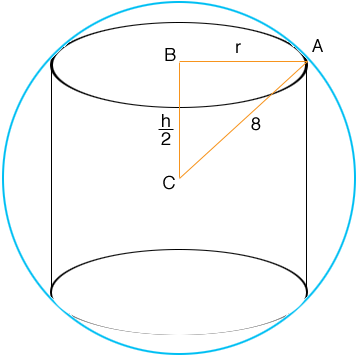
In the diagram C is the centre of the sphere and triangle ABC is a right triangle. Use Pythagoras' theorem to find a relationship between r² and h². Use this relationship to eliminate one variable in equation (1) and then use calculus to maximize the volume of the cylinder.

I hope this helps,
Penny