We have two responses for you

Hi Lucy,

I drew a diagram, but it's not to scale.

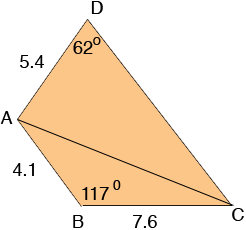
The area of the quadrilateral is the sum of the areas of the two triangles, ABC and ACD. To find the area of triangle ABC you need its height. I extended CB and dropped a perpendicular line from A to meet this line at E. The length h of AE is the height of triangle ABC. You know the measure of the angle EBA and hence you can use the sine of this angle to find h.

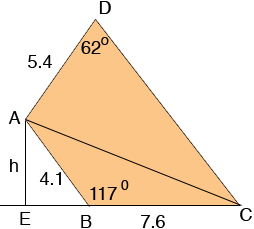
Next use the law of cosines on triangle ABC to find the length of AC. Next use the law of sines on triangle ACD to find the measure of angle ACD. The sum of the angles in a triangle is 180^o and hence you can find the measure of angle DAC. You should now be able to find the area of triangle ACD.

Penny

Hi Lucy.

Draw the diagonal AC. Now you have two triangles and if you add the areas of these two triangles, you get the area of the quadrilateral.

To get the area of a triangle, you can use Heron's Formula, but that requires knowing the lengths of all three sides (including the diagonal AC).

You can find the length of AC by using the Law of Cosines. You can then use the law of sines with triangle ACD to find the remaining two angles and the side CD.

Hope this helps,
Stephen La Rocque.