At what rate is the area of the triangle changing?

Math Central

Quandaries & Queries

Two sticks 3.5 feet long are hinged together and are stood up to form an isosceles triangle with the floor. The sticks slide apart, and at the moment when the triangle is equilateral, the angle is increasing at the rate of
1/3 radian/sec. At what rate is the area of the triangle increasing or decreasing at that moment?
Any help would be beneficiary. Thank you
Mac

Hi Mac,

Here is what I see.

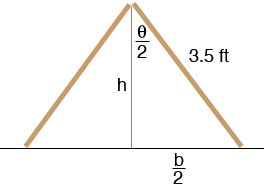
sticks

h is the height of the triangle, b is the length of the base and is the angle at the apex of the triangle. All three of these quantities are functions of time t. You know the rate of change of at a particular time and you want to know the rate of change of A, the area of the triangle, at the same time. The rate of change is the derivative with respect to t so you are going to have to find a relationship between and A.

The area of a triangle is half the base times the height so

A = b/2 h

From the diagram b/2 = 3.5 sin(/2) and h = 3.5 cos(/2). Thus

A = (3.5)² sin(/2) cos(/2)

You can now differentiate both sides with respect to t to find a relationship among A'(t), (t) and '(t). At the time when the triangle is equilateral (t) = /3 radians and '(t) = 1/3 radians per second so you can solve for A'(t).

Before you start however, do you know a trig identity that will simplify the expression for A?

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.