Mac, we have two responses for you.

Hi Mac,

I would be guided by the graphs of the sine and cosine near x = 0.

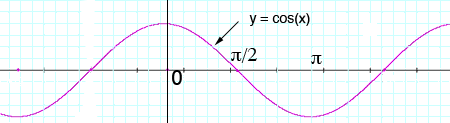
For the cosine function, when x is close to zero (actually between -π/2 and π/2), cos(x) = cos(-x) and hence near x = 0 cos(|x|) = cos(x) and thus

lim h->0 (cos|h| - cos|0|)/(h) = lim h->0 (cos(h) - cos|0|)/(h) = 0 (not 1 as you said in your question). Thus cos|x| is differentiable at x = 0.

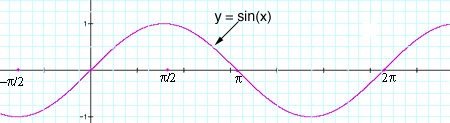
For the sine function, when x is close to zero sin(-x) = -sin(x) and hence when x is close to zero

sin|x| = sin(x) is x is positive and sin|x| = - sin(x) is x is negative.

Thus to evaluate lim h->0 (sin|h| - sin|0|)/(h) you need to consider x approaching 0 from the right and x approaching 0 from the left. These give different answers and thus the limit does not exist.

I hope this helps,
Penny

Hi Mac.

You wrote:
      

But this last step is where you erred. That's because sin|h| is positive when h is a small positive number or a small negative number near zero. But h is positive or negative, so the left limit is -1 and the right limit is +1.

The no-equations solution: Another way to think of the problem, and this doesn't even involve equations, is to consider that changing x into |x| is the same as dropping a mirror on the y axis and seeing the "negative" left half of the graph in the mirror. Then you can easily see that at x = 0, the cosine function is smooth, but the sine function has a cusp (corner), so the former is differentiable but the latter is not.

Stephen.