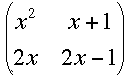A matrix of polynomials

HOME

Math Central

Quandaries & Queries

Question from Mac, a student:

can you please help me out to solve this ?

Let A be a n*n matrix, the elements of which are real (or complex) polynomial in x.
If r rows of the determinant becomes identical when x=a, then the determinant
A) has a factor of order r
B) has a factor or order > r
C) has no factor
D) has a factor of order < r

First of all i didn't understand the question properly. With the matrix, we use the coefficients of variables say x,y,z and try to find the coefficients right. so what is the meaning of "polynomial in x" ? What does that mean ?
and if the rows are identical , by the elementary row operations we can eliminate that rows right. If we do so, then the matrix wont be square matrix right ?

what is the meaning of "has a factor of order" in given solutions ?
please redirect me to some web page or book , if i have to learn anything to
understand this.
Can you please me out ?
The answer given is D !!

Hi Mac,

The matrix being described has elements that are polynomials. A 2 by 2 example might be

Notice that when x = 2 the rows are identical. The determinant of this matrix is

p(x) = x²(2x - 1) -2x(x+1)

Since the determinant has identical rows when x = 2, p(2) = 0. Hence 2 is a zero of the polynomial p(x) and the factor theorem then guarantees that x - 2 is a factor of p(x).

I hope this helps,
Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.