Hi Marsia,

I am going to show you some examples using diagrams and then give a mathematical definition. These are four functions from a set A to a set B.

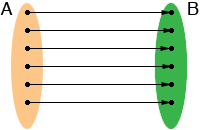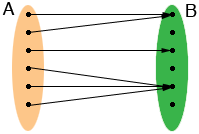
one to one	two to one
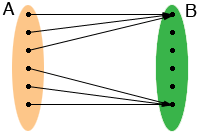
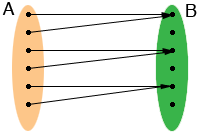
three to one	many to one

The concept of one to one I tried to illustrate in the diagrams is that if an object in B is the image of some object in A then it is the image of only one object in A.

Definition:

A function f from a set A to a set B is one to one if for any p and q in A, if f(p) = f(q) then p = q.

Example 1:

The function f(x) = 3x + 5 from the real numbers to the real numbers is a one to one.

Proof:

Suppose f(p) = f(q) then 3p + 5 = 3q + 5 and hence 3p = 3q and thus p = q.

Example 2:

The function f(x) = x² - 5x + 6 from the reals to the reals is not one to one.

Proof:

f(1) = 1 - 5 + 6 = 2 and f(4) = 16 - 20 + 6 = 2 so f(1) = f(4).

I hope this helps,
Harley