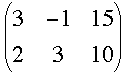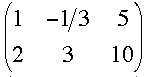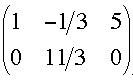Hi Mary, we hav two responses for you.

I started with the matrix

I first multiplied the first row by 1/3 to get

Now multiply the first row by -2 and add it to the second row

Can you complete it now?
Penny

Hi Mary,

An augmented matrix can be used to represent a system of equations. If we represent the two equations

3x -y =15
2x -3y =10

as a matrix of the form

3 1 15
2 -3 10

then the first column represents the x's, the second column the y's, and the last column a "constant".

Since we can add and subtract equations which are part of the same system of equations, we can do
various things to the rows and columns of the matrix. For example we can multiply every number in a
row by another non-zero constant, without changing anything about the matrix. As well, we can add or subtract one row from another without changing the matrix. To see this, let's do the following:

First, subtract the second row from the first, and re-write the matrix is transformed to:

1 4 5
2 -3 10

That's what's called a row operation, an operation on a row of a matrix. The result was obtained by
subtracting the x's in the second equation from the x's in the 1st equation, and similarly for the y's
and constants. We could also multiply the top row by a number, let's say 2:

2 8 10
2 -3 10

Now let's subtract the first row from the second row:

2 8 10
0 -11 0

What does this mean? if we write the rows of the matrix back out in their full form, we'll see that
our two equations have become:

2x +8y =10
0x -11y =0

That means that y = 0.

You should now be able to complete the problem.

The idea is to use row operations on an augmented matrix, which represents a system of equations, to reduce the system to a solvable form. In general, we want the matrix to be in "reduced row-echelon form". That means that the matrix looks like

1 0 A
0 1 B

for a 2x3 matrix, where A and B are any value. That would mean that x = A and y = B. If the equation is solvable, it is possible to get the matrix into row-echelon form by means of row-operations. If you can't get it into row echelon form, either the system is unsolveable, like:

1 0 A
0 0 B

or the system has infinitely many solutions:

1 1 A
0 0 0

where A and B are not 0. Sometimes we don't have to go all the way to reduced row echelon form, as above. In your example, we only needed to perform a few row-operations to get the system into a form which could be easily dealt with, by observing that y = 0.

Using row operations on an augmented matrix to solve a system of equations is called the Gauss-Jordan method.

Hope this helps!

Gabriel Potter